Rus dokazao teorem koji matematičari iz cijelog svijeta nisu mogli riješiti 40 godina

Dokaz je objavljen u časopisu Geometric and Functional Analysis.

"Zadatak Lászla Fejesa Tótha animira pažnju matematičara koji se bave diskretnom geometrijom preko 40 godina. Taj je zadatak imao elegantno rješenje koje smo mi uspjeli pronaći. Ono nas je navelo na misao o drugoj, jačoj hipotezi o prekrivanju sfere premještenim zonama, dobivenim presijecanjem pojedinačne lopte trodimenzionalnim trakama-pločicama, koje nisu nužno simetrične u odnosu na centar", kaže Aleksandar Poljanski, matematičar s Moskovskog fizičko-tehničkog instituta iz podmoskovskog grada Dolgoprudni.

Taj teorem, tvrde znanstvenici, najvažniji je segment takozvane diskretne geometrije, posebnog ogranka matematike koji proučava međusobne odnose geometrijskih figura. Tako on, primjera radi, može odgovoriti na pitanje koliko je najviše lopti iste veličine moguće postaviti oko jedne takve lopte. Mnoga slična pitanja imaju veliki praktični značaj, jer su izravno povezana s problemima u području IT-ja, fizike ili kemije.

Jedan od glavnih zadataka kojim se bave predstavnici ove oblasti, takozvani "teorem o pločicama", formuliran je još početkom 20. stoljeća. U najjednostavnijoj varijanti on se svodi na to da krug bilo koje veličine nije moguće prekriti pločicama čija je ukupna širina manja od dijametra same kružnice. Po pisanju Poljanskog i njegovog kolege Zilin Jianga, jednostavne varijante tog zadatka riješili su prije više od 50 godina Alfred Tarski i Thøger Bang.

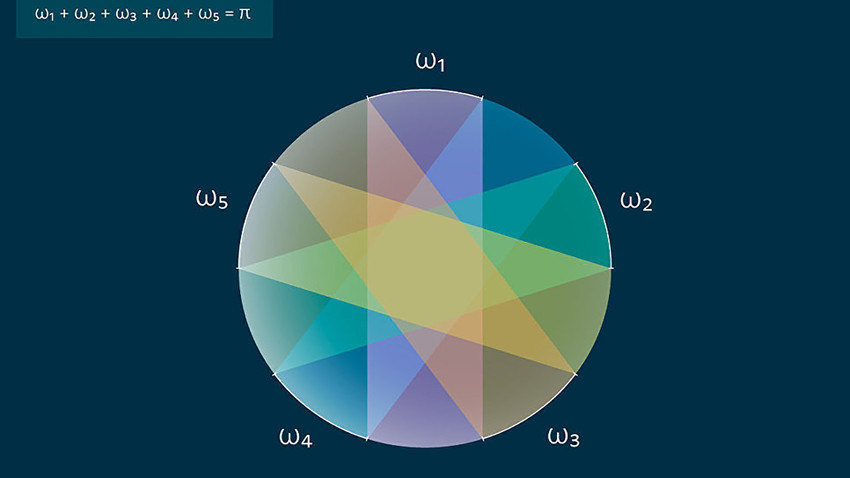
Kompliciraniju varijantu teorema je 1973. godine iznio mađarski matematičar László Fejes Tóth koji je pretpostavio da je sfernu površinu bilo koje veličine moguće prekriti proizvoljnim skupom trodimenzionalnih "pločica", čija debljina nije veća od dužine obujma.

Autori članka, koji su se oslanjali na ideju Thøgera Banga korištenu u dokazivanju prve višedimenzionalne verzije "teorema o pločicama", uspjeli su ne samo riješiti zadatak Fejesa Tótha, nego i pokazati da ona funkcionira i u višedimenzionalnom prostoru.

Matematičari su, kao i Bang, u dokazivanju išli obratno, i pretpostavili da će ukupna širina "pločica" koje potpuno pokrivaju sferu biti manja od duljine kružnice, te su željeli doćiu do kontradikcije, u vidu točke koja bi se nalazila na sferi, a ne bi bila prekrivena zonama.

Takve kontradikcije su pronađene, čime je dokazana ispravnost ideja mađarskog matematičara. Istraživači vjeruju da će njihov dokaz ubrzati razvoj diskretne geometrije i omogućiti formiranje niza novih matematičkih i praktičnih zadataka u vezi s "poučkom o pločicama".